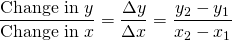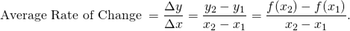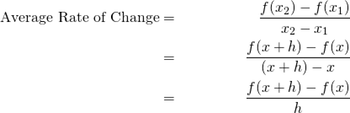kecepatan rata-rata dan sesaat
Apa itu kalkulus diferensial ? Ayo jalan-jalan dan cari tahu!
Misalkan kita melakukan perjalanan dari New York, NY ke Boston, MA. Itu sekitar 200 mil dan (tergantung lalu lintas), itu akan memakan waktu sekitar empat jam. Sekarang, kita semua tahu bahwa jarak sama dengan kecepatan kali waktu, atau d = rt . Dalam contoh ini, kami memiliki jarak dan waktu, dan kami menafsirkan kecepatan (atau kelajuan) sebagai laju perubahan. Jadi kita bisa menghitung kecepatan rata -rata kita selama perjalanan dengan membagi jarak dengan waktu. Itu dia:
(200 mil) / (4 jam) = 50 mil / jam
Namun, jika Anda pernah mengemudi di Boston atau New York, Anda tahu bahwa saat berada di kota, kecepatan Anda kurang dari 50 mph. Di sisi lain, saat Anda memasuki jalan raya, perkirakan akan melaju lebih dari 50 mph. Perhitungan yang kami lakukan hanyalah rata-rata dan menjawab pertanyaan: jika kecepatan saya tetap sama sepanjang perjalanan, apakah itu?
Tapi mobil Anda lebih tahu. Ini memiliki speedometer yang melacak kecepatan (velocity) pada saat tertentu. Saat Anda melihat spidometer dan terbaca 61 mph, itu memberi tahu Anda kecepatan sesaat pada saat tertentu saat Anda memutuskan untuk melihatnya. Bagaimana Anda tahu? Mobil Anda melakukan sesuatu seperti kalkulus diferensial untuk menyelesaikannya!
Definisi
Kalkulus diferensial adalah studi tentang laju perubahan fungsi, menggunakan alat limit dan turunan.
Sekarang saya tahu bahwa beberapa kata ini mungkin asing bagi Anda pada saat ini dalam perjalanan Anda, tetapi kami akan meluangkan waktu untuk menjelaskannya dalam pelajaran ini. Ingat, ini hanyalah pengantar topik penting kalkulus diferensial. Seluruh perawatan membutuhkan waktu satu semester atau lebih untuk dijelaskan!
Nilai tukar
Oke, mari kita gali lebih dalam ide-ide ini. Ada dua konsep terkait untuk dibahas, laju perubahan rata-rata dan laju perubahan sesaat.
biaya rata-rata
Tarif rata-rata dimulai dengan gagasan a y = f ( x ). Masukkan x dan dapatkan keluaran y . Misalkan Anda mengetahui ini dari aljabar atau prakalkulus. Dalam kalkulus, laju perubahan adalah ukuran bagaimana nilai y dari suatu fungsi berubah sehubungan dengan perubahan nilai x . Kedengarannya membingungkan? Nah, mari kita pikirkan tentang kecepatan dengan cara yang sama. Ini adalah pecahan, dengan perubahan y di bagian atas dibagi dengan perubahan x di bagian bawah.
Misalkan kita mulai dari x1 dan berakhir di x2 . Jadi perubahan x adalah selisihnya, x2 – x1 , yang mirip dengan nilai y seperti yang kita lihat di sini. Notasi segitiga adalah delta modal Yunani , yang berarti “perubahan” kuantitas.
|
|
Ini bukan hal baru. Ini adalah rumus kemiringan yang sama dengan yang Anda lihat di kelas aljabar! Itu hanya bangun dari berlari. Dan itu mengukur apa yang kita sebut tingkat rata-rata perubahan f selama interval dari x1 ke x2 . Satu-satunya perbedaan sekarang adalah kita harus menggunakan fungsi yang diberikan f untuk menemukan nilai-y , seperti:
|
|
tarif instan
Baik, tapi bagaimana jika kita ingin mengetahui kurs pada saat tertentu, atau kurs instan kita? Rumus laju perubahan rata-rata memerlukan dua titik yang berbeda, x1 dan x2 , dan rumus ini tidak berfungsi dengan baik ketika x1 = x2 karena x2 – x1 = 0 di bagian bawah pecahan. Dan kita tidak pernah diizinkan untuk membagi dengan 0, kan?
Di sinilah batas masuk. Anda lihat, meskipun kami tidak diizinkan untuk membiarkan x2 = x1 (karena itu akan menghasilkan pembagian dengan 0, kami dapat mengizinkan x2 untuk semakin dekat dan semakin dekat dengan x1 .
Namun, detailnya menjadi rumit di sini. Katakanlah kita memperbaiki x1 = x (untuk beberapa nilai arbitrer x ), dan biarkan x2 = x + (sedikit). Jadi jika bitnya cukup kecil, perhitungan kecepatan rata-rata harus menjadi perkiraan yang cukup akurat dari kecepatan sesaat di x . Sekarang, daripada mengatakan ‘sedikit’, mari gunakan variabel, seperti h . Artinya, x2 = x + h . Jadi, rumus laju perubahan terlihat seperti ini:
|
|
Terakhir, kita harus berasumsi bahwa h pada akhirnya akan mendekati 0 (walaupun dalam praktiknya, ini hanya dapat terjadi setelah beberapa aljabar digunakan untuk menyederhanakan ekspresi). Kami menulis ini menggunakan notasi limit, dan ini menjadi definisi laju perubahan sesaat , atau turunan dari f , dengan definisi limit dari turunannya terlihat seperti ini:
|
|
Derivatif dan diferensiasi
Sekarang setelah kaki kita sedikit basah, mari kita bicara lebih banyak terminologi. Laju perubahan sesaat dari suatu fungsi disebut turunan dari fungsi tersebut, seperti yang kami sebutkan beberapa menit yang lalu. Dalam pelajaran selanjutnya, Anda akan mengembangkan alat dan rumus untuk membantu menemukan turunan. Misalnya, jika f ( x ) = x ^ 2 , maka sesuatu yang disebut aturan pangkat menyiratkan bahwa turunannya adalah f ( x ) = 2. Dan proses menemukan turunannya disebut diferensiasi .
Ada banyak teknik berbeda yang digunakan untuk membedakan fitur. Ada juga banyak aplikasi berbeda untuk kalkulus diferensial! Dengan demikian, kalkulus diferensial dapat dianggap sebagai cabang matematika di mana seseorang mempelajari bagaimana dan mengapa membedakan fungsi.
Ringkasan Pelajaran
Ok, mari kita tinjau dengan cepat. Kalkulus diferensial adalah cabang matematika yang berhubungan dengan laju perubahan. Idenya dimulai dengan rumus laju perubahan rata-rata, yang pada dasarnya merupakan perhitungan kemiringan. Kemudian, dengan menggunakan batasan, rumus laju perubahan sesaat dapat dikembangkan, yang disebut turunan fungsi.