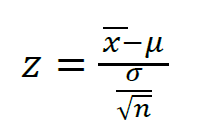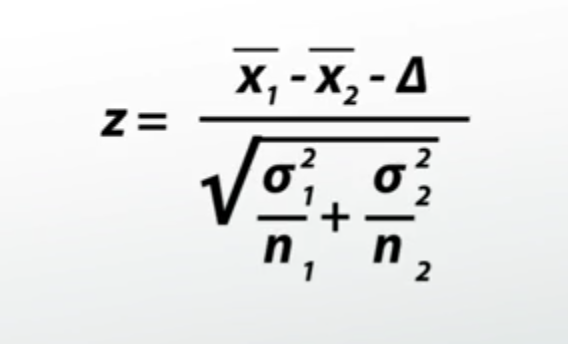Tes Z dan Drive-Thrus
Rantai makanan cepat saji Speedy Burger mengklaim bahwa pelanggannya dapat berharap untuk menyelesaikan pesanan swalayan, sejak mereka memesan hingga menerima makanan mereka, dalam 90 detik dengan standar deviasi 5 detik. Ini berarti bahwa rata-rata pelanggan dapat berharap mendapatkan makanan yang lezat dalam waktu sekitar satu setengah menit. Chill Hot Dog, perusahaan makanan cepat saji pesaing, ingin membantah klaim ini, jadi mereka mengirim beberapa mata-mata dengan stopwatch untuk menghitung waktu sampel acak dari 50 pelanggan yang memesan melalui drive-thru Speedy Burger. Melalui pengamatan, mereka menemukan bahwa waktu rata-rata untuk menerima pesanan yang sudah selesai adalah 102 detik. Apakah bukti ini cukup untuk membantah klaim Speedy Burger? Untuk mengetahuinya, Anda dapat melakukan uji z.
Tes Z adalah perhitungan yang sangat berguna ketika membandingkan sampel dan populasi berarti untuk menentukan apakah ada perbedaan yang signifikan secara statistik. Lagi pula, perbedaan antara sampel dan rata-rata populasi mungkin karena kebetulan. Perhitungan ini dapat digunakan untuk membuktikan atau menyangkal pernyataan atau hipotesis. Mereka membutuhkan sampel acak dari populasi yang terdistribusi normal dan memiliki mean (rata-rata) yang diketahui. Tes Z paling berguna dalam populasi besar, di mana ukuran sampel lebih besar dari 30. Mari pelajari lebih lanjut tentang metode statistik yang berguna ini dan rumus yang digunakan.
Jenis yang berbeda
Ada berbagai uji-z yang dapat digunakan untuk tujuan yang berbeda, tetapi dua yang paling umum adalah uji-z satu sampel dan uji-z dua sampel . Seperti namanya, uji z satu sampel membandingkan rata-rata sampel dan uji z dua sampel membandingkan dua. Tes Z terutama digunakan ketika ada sampel yang lebih besar ( n > 30), tetapi tidak peduli uji z mana yang digunakan, semuanya membutuhkan data dengan distribusi normal, artinya data terdistribusi secara merata di sekitar rata-rata.
Formula uji Z satu sampel
Mari jelajahi contoh di mana z-test dapat digunakan untuk mencoba menyangkal klaim. Ingat klaim waktu Speedy Burger? Mereka telah memutuskan untuk membuktikan kepada Chill Hot Dog, sekali dan untuk selamanya, bahwa apa pun yang dilaporkan mata-mata mereka, klaim 90 detik Speedy Burger adalah benar. Untuk melakukannya, mereka melakukan beberapa perhitungan z-test.
Karena mereka akan membandingkan data yang ada untuk waktu drive-thru dengan sampel acak pelanggan yang diamati oleh pesaing mereka, mereka harus menggunakan uji-z satu sampel. Rumusnya adalah:
|
|
Di mana:
|
|
Mengganti data ke dalam rumus menghasilkan z-score , yang disebut nilai kritis. Skor z adalah nilai yang kita lihat untuk menentukan apakah hipotesis itu benar. Skor z di sini ternyata 16,97. Apa arti skor z ini? Artinya, sampel tertentu adalah 16,97 standar deviasi di atas rata-rata, yang berarti bahwa untuk sampel tertentu ini rata-rata memiliki nilai di atas rata-rata standar. Untuk Speedy Burger, itu berarti, rata-rata, mereka tidak memenuhi klaim 90 detik. Jika skor-z cukup rendah, meskipun berada di atas rata-rata standar, itu masih berarti bahwa Speedy Burger memenuhi klaim 90 detik. Namun sayangnya, skor-z Speedy Burger jauh lebih tinggi.
Uji Z Dua Sampel
Jika diperlukan untuk membandingkan dua populasi yang berdistribusi normal tetapi independen, dan standar deviasi diketahui, kita dapat menggunakan uji z dua sampel. Katakanlah, misalnya, kita ingin menentukan siapa yang lebih mungkin memberikan suara dalam suatu pemilihan: laki-laki atau perempuan. Ini akan melibatkan perbandingan dua populasi independen, sehingga uji z dua sampel akan sesuai. Rumus untuk uji z dua sampel mirip dengan uji z satu sampel:
|
|
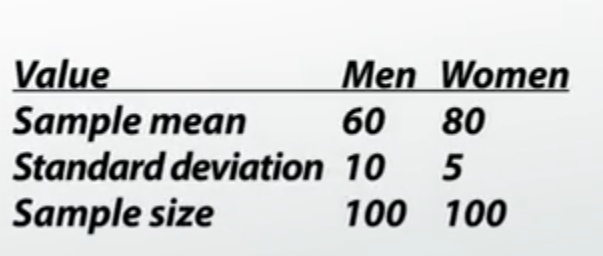
Simbol delta di sini mewakili perbedaan yang dihipotesiskan antara kedua sampel. Katakanlah kita memiliki informasi ini untuk pria dan wanita yang memilih:
|
|
Jika asumsinya adalah bahwa laki-laki dan perempuan memiliki kemungkinan yang sama untuk memilih, maka delta di sini adalah nol, karena asumsinya adalah tidak ada perbedaan. Memasukkan nilai-nilai ini dalam menggunakan Sampel 1 sebagai pria dan Sampel 2 sebagai wanita, kami mendapatkan skor-z ini:
|
|
Kami mendapatkan skor-z negatif, karena kami mengurangi wanita dari pria dan rata-rata sampel untuk wanita lebih tinggi daripada pria. Sejauh memahami skor-z, tidak masalah apakah itu negatif atau positif, karena skor-z kami lebih rendah dari rata-rata standar dan itu bukan angka yang sangat kecil, ini memberi tahu kami bahwa hipotesis kami bahwa pria dan wanita sama-sama mereka memilih sama tidak benar.
Namun pada kenyataannya, uji z dua sampel tidak umum digunakan karena standar deviasi dua populasi tidak diketahui secara umum.
Ringkasan Pelajaran
Dalam pelajaran ini, kita telah belajar tentang uji z , yang merupakan perhitungan statistik yang berguna jika kita mengetahui standar deviasi. Tes ini umumnya digunakan ketika kita memiliki ukuran sampel yang besar di mana n > 30 dan menganggap data berdistribusi normal. Uji z satu sampel membandingkan rata-rata sampel, dan uji z dua sampel membandingkan rata-rata dua sampel. Rumusnya adalah:
|
|
Skor z , disebut nilai kritis, adalah nilai yang kita lihat untuk menentukan apakah hipotesis itu benar.