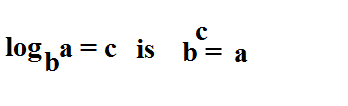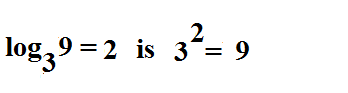Definisi Bentuk Eksponensial
Bentuk eksponensial dari ekspresi aljabar adalah ekspresi yang menyertakan eksponen. Ekspresi apa pun yang menyertakan eksponen dikatakan ditulis dalam bentuk eksponensial. Berikut adalah beberapa contoh untuk membiasakan Anda:
x^2
3y^5 2^3
Konversi ke bentuk eksponensial
Dalam aljabar, seringkali ada cara berbeda untuk menyatakan hal yang sama. Bentuk yang Anda pilih untuk digunakan bergantung pada apa yang akan membuat masalah yang Anda kerjakan lebih mudah dipecahkan atau memberi Anda solusi yang dapat digunakan oleh orang lain. Mari kita lihat contoh sederhana:
Ubah 8 menjadi bentuk eksponensial.
8 = 2*2*2 = 2^3
Ekspresi sederhana ini paling baik digunakan jika Anda mencoba memfaktorkan sebuah ekspresi dan ingin mengetahui berapa banyak 2 yang dikalikan bersama sama dengan 8.
Mengonversi ekspresi ke bentuk eksponensial juga berguna saat Anda mencoba menambahkan suku sejenis atau menyederhanakan ekspresi. Sebagai contoh:
Sederhanakan berikut ini:
2x ^ 4 + x * x * x * x
x * x * x * x = x ^ 4 ditulis dalam bentuk eksponensial , kita dapat menyederhanakan pernyataan tersebut menjadi persamaan. Hasil dari penyederhanaan itu adalah 2 x ^4 + x ^4. Sekarang bisa disederhanakan lagi karena suku-sukunya mirip dan bisa dijumlahkan. Hasilnya adalah 3x^ 4.
bentuk logaritma
Logaritma mengacu pada eksponen dalam ekspresi aljabar yang ditulis dalam bentuk eksponensial . Ekspresi logaritmik adalah kebalikan dari ekspresi eksponensial. Logaritma (log) diperkenalkan pada abad ke-17 sebagai cara yang lebih mudah untuk menyelesaikan ekspresi aljabar dan dengan cepat diadopsi oleh para ilmuwan, insinyur, dan lainnya untuk mempermudah perhitungan.
Aturan untuk mengubah ekspresi yang ditulis dalam bentuk logaritmik menjadi ekspresi yang ditulis dalam bentuk eksponensial adalah:
|
|
Untuk mengonversi ekspresi dalam bentuk eksponensial menjadi bentuk logaritmik, cukup isi a , b , dan c ke tempatnya yang tepat. Mari kita coba.
Ubah 3^2 = 9 menjadi bentuk logaritmik.
Untuk melakukan ini, cukup masukkan angka di tempatnya masing-masing, seperti:
|
|
Alasan ingin mengonversi satu bentuk ke bentuk lainnya sama dengan yang telah dibahas di atas. Ada kasus di mana lebih mudah untuk menyelesaikan atau memanipulasi ekspresi berdasarkan bentuknya. Bentuk logaritmik lebih mudah digunakan saat menyelesaikan eksponen karena ada kalkulator dan tabel data yang menyederhanakan prosesnya. Sebagai contoh:
Selesaikan 10^x = 37
Jadi, persamaan ini tampaknya mustahil untuk dipecahkan; setidaknya, bukan tanpa banyak pekerjaan. Kita tahu bahwa 10^2 = 100, jadi jawabannya harus berupa angka desimal antara 1 dan 2. Kita bisa terus menebak-nebak dan mencoba-coba sampai mendapatkan jawabannya, atau kita bisa mengubah soal menjadi log, gunakan kalkulator , dan itu akan selesai dalam hitungan detik. Karena basis, atau b dalam ungkapan ini, adalah 10, ini juga dikenal sebagai logaritma biasa dan dapat diselesaikan hanya dengan menggunakan kalkulator. Pertama, ubah ekspresi menjadi read log(37) = x . Dalam hal ini, 10 dipahami dan tidak perlu ditulis. Kemudian selesaikan x menggunakan kalkulator Anda. x = 1,57. Itu berarti 10^(1,57) = 37.
Ringkasan Pelajaran
Ekspresi yang ditulis dalam bentuk eksponensial ditulis dengan eksponen. Bentuk eksponensial juga kebalikan dari bentuk logaritmik. Saat mencoba menyelesaikan persamaan yang eksponennya tidak diketahui, akan lebih mudah untuk mengubah persamaan dari bentuk eksponensial ke bentuk logaritmik.
hasil pembelajaran
Ketika Anda selesai dengan pelajaran ini, Anda harus dapat:
- Kenali persamaan eksponensial
- Ubah persamaan eksponensial menjadi bentuk logaritmik
- Selesaikan persamaan eksponensial