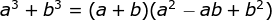Definisi
Kubus sempurna adalah ekspresi apa pun yang dapat mewakili volume kubus. Bayangkan merogoh keranjang mainan dan mengeluarkan beberapa balok bangunan, lalu mencoba memasukkan balok-balok itu ke dalam ember. Katakanlah Anda menggambar 4 balok. Anda dapat membuat persegi 2 balok kali 2 balok dengan 4 balok, tetapi tingginya hanya 1 balok, jadi tidak akan menjadi kubus. Untuk membuat kubus, Anda perlu mengeluarkan 4 balok lagi untuk diletakkan di atas persegi yang Anda buat, seperti ini:
|
|
Sekarang, kamu memiliki volume 8 balok yang membentuk sebuah kubus yang panjang, lebar, dan tingginya semuanya 2. Jadi, 8 adalah bilangan kubus sempurna karena 2 x 2 x 2 = 8 atau 2^3 = 8.
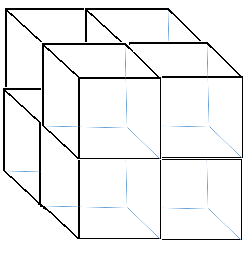
Misalkan Anda ingin memperbesar ukuran kubus sehingga memiliki 3 balok di setiap sisinya, sehingga terlihat seperti ini:
|
|
Jadi, Anda membutuhkan 19 balok lagi dengan total 27 balok, karena 3 x 3 x 3 = 3^3 = 27.
Semua kubus sempurna dihasilkan dari menaikkan bilangan bulat , bilangan bulat atau pasangan negatifnya, atau variabel pangkat tiga. Ekspresi ini disebut kubus karena volume kubus ditemukan dengan menaikkan panjang sisinya dengan pangkat tiga.
Binomial kubus sempurna adalah ekspresi yang terdiri dari dua suku yang merupakan kubus sempurna . Istilah-istilah ini ditambahkan atau dikurangi satu sama lain.
Memfaktorkan binomial kubus sempurna
Faktor adalah ekspresi yang dikalikan bersama. Jadi, pemfaktoran meminta Anda untuk memecah ekspresi menjadi ekspresi yang lebih sederhana yang dikalikan. Faktor-faktor binomial kubus sempurna mungkin tidak tampak sangat sederhana karena pada akhirnya menjadi binomial , dua suku ditambahkan atau dikurangi, dikalikan dengan trinomial , tiga suku ditambahkan atau dikurangi. Namun, ada rumus yang memberi Anda faktor dengan cukup mudah.
Ketika Anda dihadapkan dengan berbagai masalah pemfaktoran, Anda memiliki metode yang berbeda untuk mendekati ekspresi yang berbeda. Pastikan untuk menerapkan strategi yang benar untuk setiap jenis masalah. Binomial kubus sempurna cukup mudah diidentifikasi dan selalu dapat difaktorkan menggunakan rumus ini. Petunjuk pertama Anda adalah bahwa selalu ada dua suku dan variabel memiliki eksponen yang merupakan kelipatan 3. Setelah Anda melihat fitur tersebut, Anda akan ingin memeriksa bahwa koefisien (angka dikalikan dengan variabel) dan konstanta (angka tanpa variabel) dari kedua istilah adalah bilangan kubik sempurna.
Setelah Anda yakin memfaktorkan binomial kubus sempurna, Anda akan menggunakan rumus ini:
|
|
Berikut petunjuknya: jika Anda memiliki selisih kubus dalam bentuk a ^3 – b ^3, anggap saja sebagai a ^3 + (- b ^3). Dengan begitu Anda hanya perlu menghafal rumus ini.
contoh
Mari kita lihat beberapa contoh:
Contoh 1
Faktor: x ^3 + 64
Dalam soal ini, kita melihat bahwa dua suku telah ditambahkan, menjadikannya binomial. Kedua istilah tersebut adalah kubus sempurna. Kita dapat mengetahuinya dari pangkat 3 per x , dan kita tahu bahwa 64 adalah kubus sempurna karena kubus berukuran 4 x 4 x 4 memiliki volume 4 ^ 3 = 64. Untuk memfaktorkan pernyataan tersebut, kita lakukan hal berikut :
- menentukan apa a dan b untuk formula kami. Suku pertama mudah, x adalah a . Pada suku kedua, 64 = 4^3, jadi b adalah 4.
- Lalu, kita masukkan nilai tersebut ke dalam rumus: ( x + 4) ( x ^ 2 – ( x ) (4) + 4 ^ 2).
- Kita dapat menulis ulang ( x ) (4) menjadi 4 x , dan mengevaluasi eksponen pada suku terakhir untuk membersihkannya. Bentuk faktor terakhir kita adalah: ( x + 4) ( x ^ 2 – 4 x + 16).
Contoh 2
Ini contoh lainnya. Faktor: 8 x ^ 3 – 125
Dalam soal ini, kita melihat bahwa dua suku dikurangkan satu sama lain, menjadikannya binomial. Kekuatan 3 dalam x memberi tahu kita bahwa kemungkinan besar kita berurusan dengan pasangan kubus yang sempurna. Mari kita periksa angka-angkanya untuk memastikannya adalah kubus yang sempurna. Angka 8 adalah kubus sempurna karena, seperti yang telah kita bahas di awal pelajaran ini, 2^3 = 8. Angka 125 adalah kubus sempurna karena kubus berukuran 5 x 5 x 5 akan memiliki volume 5^3 = 125.
Untuk memfaktorkan ekspresi, kami melakukan hal berikut:
- menentukan apa a dan b untuk rumus kami. Kali ini di suku pertama, 8 x ^ 3 = (2 x ) ^ 3. Jadi, a adalah 2 x . Pada suku kedua kali ini negatif, -125 = (-5)^3, jadi b adalah -5.
- Lalu, kita masukkan nilai tersebut ke dalam rumus: (2 x + (-5)) ((2 x ) ^ 2 – (2 x ) (- 5) + (-5) ^ 2).
- Kita perlu sedikit membersihkan persyaratannya. Pada faktor binomial (2 x + (-5)), kita dapat menggabungkan tanda plus dan negatif menjadi (2 x – 5). Dalam faktor trinomial, suku pertama (2 x ) ^ 2 dapat dievaluasi sebagai 4 x ^ 2. Pada suku berikutnya, kita dapat mengalikan (2 x ) dan (-5) bersama-sama untuk mendapatkan (-10 x ). Karena suku itu dikurangi, alih-alih menggunakan negatif ganda – (- 10 x ), kita dapat menulis +10 x . Pada suku terakhir, kita mengkuadratkan (-5), yang menghasilkan 25. Jadi, bentuk pemfaktoran akhirnya adalah (2 x – 5) (4 x ^ 2 + 10 x + 25).
Contoh 3
Inilah contoh terakhir. Faktor: 27 x ^ 6 – 343 y ^ 3
Dalam soal ini, kita memiliki dua suku yang dikurangkan satu sama lain, menjadikannya binomial. Mari kita periksa apakah semuanya adalah kubus yang sempurna. 27 adalah kubus sempurna karena, seperti yang telah kita bahas di awal pelajaran ini, 3^3 = 27. 343 mungkin memerlukan sedikit kalkulus, tetapi merupakan kubus sempurna karena kubus berukuran 7 x 7 x 7 akan memiliki volume dari 7^3 = 343. Sekarang, mari kita lihat eksponennya. Y ^3 jelas merupakan kubus sempurna, tapi bagaimana dengan x ^ 6? Ingatlah bahwa setiap pangkat yang merupakan kelipatan 3 juga merupakan kubus sempurna. Dalam hal ini, kita harus menganggap x ^6 sebagai ( x ^2)^3.
Untuk memfaktorkan ekspresi, kami melakukan hal berikut:
- menentukan apa a dan b untuk rumus kami. Pada suku pertama, 27 x ^ 6 = (3 x ^ 2) ^ 3. Jadi, a adalah 3 x ^ 2. Suku kedua kali ini negatif, -343 y ^ 3 = (-7 y ) ^ 3, jadi b adalah -7 y.
- Lalu, kita masukkan nilai tersebut ke dalam rumus: (3 x ^ 2 + (-7 y )) ((3 x ^ 2) ^ 2 – (3 x ^ 2) (-7 y ) + (-7 y ) ^ 2 .
- Seperti pada contoh sebelumnya, kita perlu membersihkan persyaratannya. Dalam faktor binomial, kita dapat menggabungkan plus dan minus untuk menulis (3 x ^ 2 – 7 y ). Dalam faktor trinomial, suku pertama (3 x ^ 2) ^ 2 dapat dievaluasi sebagai 9 x ^ 4. Pada suku berikutnya, kita dapat mengalikan (3 x ^ 2) dan (-7 y ) bersama-sama untuk mendapatkan (- 21 ( x ^ 2) y ). Karena suku itu dikurangi, alih-alih menggunakan negatif ganda, kita bisa menulis +21 ( x ^ 2) y . Pada suku terakhir, kita mengkuadratkan (-7 y ), yang menghasilkan 49 y ^ 2. Jadi, bentuk pemfaktoran akhirnya adalah (3 x ^ 2-7 y ) (9 x ^ 4 + 21 ( x ^ 2) dan + 49 dan ^ 2).
Ringkasan Pelajaran
Binomial kubus sempurna memiliki dua suku yang merupakan kubus sempurna. Untuk memfaktorkan salah satu dari binomial ini, pertama-tama identifikasi a dan b untuk rumus tersebut dengan menghitung pangkat tiga dalam setiap suku. Kemudian lengkapi rumusnya:
a ^3 + b ^3 = ( a + b ) ( a ^ 2 – ab + b ^ 2)
Terakhir, bersihkan perkalian dan eksponen. Jawaban Anda akan selalu memiliki dua faktor, binomial dan trinomial.
istilah kunci
- kubus sempurna: ekspresi apa pun yang dapat mewakili volume kubus
- bilangan bulat: bilangan bulat atau pasangan negatifnya
- kubus sempurna binomial: ekspresi yang terdiri dari dua suku yang merupakan kubus sempurna
- faktor: ekspresi yang dikalikan bersama
- pemfaktoran: memecah ekspresi menjadi ekspresi yang lebih sederhana yang dikalikan
- binomial: dua istilah ditambahkan atau dikurangi
- trinomial: tiga istilah ditambahkan atau dikurangi
- koefisien: angka dikalikan dengan variabel
- konstanta: angka tanpa variabel
|
|
|
8 adalah bilangan kubik sempurna karena 2 x 2 x 2 = 8 atau 2^3 = 8. |
hasil pembelajaran
Setelah melihat pelajaran ini, Anda harus dapat mencapai tujuan berikut:
- Mendefinisikan binomial kubus sempurna
- Faktorkan binomial kubus sempurna