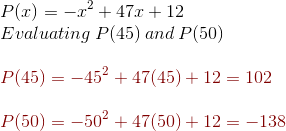Prinsip lokasi
Misalkan ada hutan di dekat rumah Anda yang baru-baru ini dihuni oleh tupai langka. Para ilmuwan telah melacak populasi tupai selama setahun terakhir dan, dengan mempertimbangkan sumber daya alam dan ruang, telah mengembangkan fungsi berikut untuk memodelkan bagaimana populasi tupai akan berubah dari waktu ke waktu.
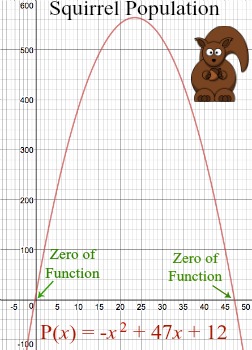
- P ( x ) = – x 2 + 47 x + 12, dimana x = jumlah bulan sejak ilmuwan mulai mengamati tupai.
Perhatikan bahwa P ( x ) adalah fungsi polinomial. Polinomial adalah ekspresi matematis dari jumlah suku yang mengandung variabel yang sama yang dipangkatkan berbeda.
Tupai-tupai ini sangat lucu, jadi Anda berharap mereka akan ada untuk sementara waktu. Ini membuat orang bertanya-tanya kapan tupai akan meninggalkan hutan menurut model populasi. Kapan populasi akan mencapai nol? Berbicara secara matematis, Anda ingin mengetahui angka nol dari polinomial.
Nol polinomial adalah nilai x yang memberikan nilai y nol saat dihubungkan ke polinomial. Secara grafis, nol dari fungsi polinomial adalah tempat fungsi memotong sumbu x karena di sinilah nilai fungsi sama dengan nol.
Mengetahui hal ini, buat sketsa grafik fungsi para ilmuwan dan lihat di mana ia melintasi sumbu x .
|
|
Sepertinya populasi tupai akan mencapai nol antara 45 dan 50 bulan, tetapi jumlah bulan yang tepat sulit untuk ditentukan.
sumbu x di nol fungsi, nilai y berubah dari positif ke negatif atau dari negatif ke positif. Ini mengarah pada aturan yang berguna yang disebut prinsip lokasi.
Prinsip lokasi untuk nol fungsi polinomial menyatakan bahwa jika kita memiliki fungsi polinomial f ( x ) dan jika f ( a ) > 0 dan f ( b ) < 0, maka f ( x ) memiliki setidaknya satu nol antara a dan b . Itu berbicara mewah dari fakta bahwa jika nilai fungsi polinomial berubah tanda antara x = a dan x = b , maka fungsi tersebut harus memiliki nol antara x = a dan x = b .
Untuk mengilustrasikan hal ini, pertimbangkan bahwa tampaknya populasi tupai akan mencapai nol dalam 45-50 bulan. Jika kita memasukkan nilai-nilai ini ke dalam fungsi populasi, kita mendapatkan P (45) = 102 dan P (50) = -138.
|
|
Perhatikan bahwa nilai fungsi berubah dari positif ke negatif antara x = 45 dan x = 50. Oleh karena itu, fungsi polinomial memiliki nol antara x = 45 dan x = 50.
Perkiraan nol dari tabel
Sekarang, seperti yang kami katakan, sulit untuk menentukan jumlah pasti bulan berdasarkan grafik, dan rentang 5 bulan 45-50 bulan adalah waktu yang cukup lama. Untungnya, kita dapat menggunakan prinsip lokasi untuk mempersempitnya lebih jauh dan memperkirakan dengan lebih akurat di mana nol dari fungsi polinomial akan muncul.
Kita tahu bahwa nol akan terjadi antara nilai x apa pun a dan b , di mana nilai fungsi berubah tanda, sehingga kita dapat membuat tabel nilai fungsi dari nilai x 45 menjadi 50, lalu temukan perubahan tanda antara nilai-nilai fungsi . Kemudian kita tahu bahwa terjadi nol di antara nilai x yang sesuai dengan nilai fungsi tempat terjadinya perubahan tanda.
|
x |
P ( x ) |
|
Empat.Lima |
102 |
|
46 |
58 |
|
47 |
12 |
|
48 |
-36 |
|
49 |
-86 |
|
lima puluh |
-138 |
Dari tabel, kita melihat bahwa P (47) = 12 dan P (48) = -36, dan nilai fungsi berubah dari positif ke negatif antara x = 47 dan x = 48. Oleh karena itu, dengan prinsip lokasi, kita tahu fungsi polinomial memiliki nol antara x = 47 dan x = 48. Hal ini memberitahu kita bahwa tupai akan benar-benar hilang dalam 47-48 bulan. Itu pasti mempersempitnya lebih akurat!
Contoh lain
Mari kita lihat satu contoh lagi. Misalkan kita bekerja dengan fungsi polinomial berikut:
f ( x ) = x 3 + 5 x 2 – 3 x – 10
Kami memiliki tabel nilai fungsi untuk berbagai nilai x sebagai berikut:
|
x |
-6 |
-5 |
-4 |
-3 |
-dua |
-1 |
0 |
1 |
dua |
|
f ( x ) |
-28 |
5 |
18 |
17 |
8 |
-3 |
-10 |
-7 |
12 |
Berdasarkan tabel dan prinsip lokasi, dapatkah Anda memperkirakan berapa angka nol yang dimiliki fungsi polinomial ini, dan kira-kira di mana letaknya?
Kita tahu bahwa nol terjadi di mana pun ada perubahan tanda pada nilai fungsi. Dari tabel tersebut, kita dapat melihat bahwa ada tiga tempat terjadinya hal ini. Dari x = -6 ke x = -5, f ( x ) berubah dari negatif ke positif (-28 ke 5). Dari x = -2 ke x = -1, f ( x ) berubah dari positif ke negatif (8 ke -3). Akhirnya, dari x = 1 ke x = 2, f ( x ) berubah dari negatif ke positif (-7 ke 12).
Dengan prinsip lokasi, kita mendapatkan bahwa fungsi tersebut memiliki tiga angka nol yang terjadi antara x = -6 dan x = -5, x = -2 dan x = -1, dan x = 1 dan x = 2. Wow! Semua informasi itu dari tabel nilai! Prinsip lokasi ini sangat berguna!
Ringkasan Pelajaran
f ( x ) adalah fungsi polinomial ketika itu adalah ekspresi matematika dari jumlah suku yang mengandung variabel yang sama yang dipangkatkan berbeda. Angka nol dari fungsi polinomial adalah nilai x yang menjadikan f ( x ) = 0 benar.
Prinsip letak nol polinomial menyatakan bahwa jika nilai suatu fungsi polinomial berubah tanda antara x = a dan x = b , fungsi tersebut harus memiliki nol antara x = a dan x = b . Kita dapat menggunakan prinsip ini untuk memperkirakan nol fungsi polinomial, yang sangat berguna dalam aplikasi dunia nyata seperti keuangan, astronomi, geologi, arsitektur, atau fisika, hanya untuk beberapa nama! Mari kita simpan prinsip ini di kotak peralatan matematika kita, sehingga kita dapat menariknya keluar dan menggunakannya kapanpun kita membutuhkannya!