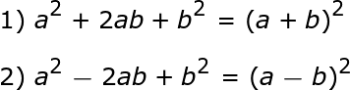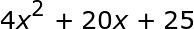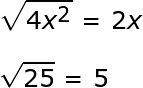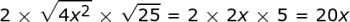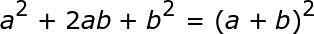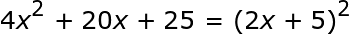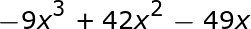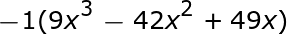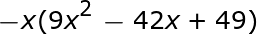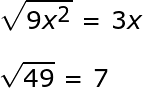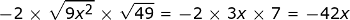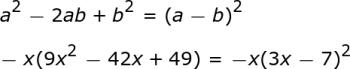Apa itu trinomial kuadrat sempurna?
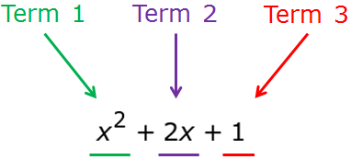
Dalam kursus aljabar, Anda akan menghabiskan banyak waktu bekerja dengan polinomial. Kami mengklasifikasikan polinomial ini sesuai dengan jumlah istilah yang dikandungnya. Misalnya, trinomial adalah polinomial yang memiliki tiga suku.
|
|
Apa yang Anda akan menemukan Anda menghabiskan sebagian besar waktu Anda dengan trinomial adalah memfaktorkan mereka untuk menyelesaikan yang tidak diketahui. Dalam pelajaran ini, kita akan mempelajari cara memfaktorkan jenis trinomial khusus yang disebut trinomial kuadrat sempurna . Trinomial kuadrat sempurna memiliki dua bentuk berikut:
|
|
Di sebelah kiri tanda sama dengan adalah trinomial yang akan diberikan kepada Anda, dan di sebelah kanan adalah bentuk faktornya. Suku-suku yang menyusun trinomial kuadrat sempurna kita dapat dibagi menjadi komponen a dan b . Kedua komponen ini dapat terdiri dari konstanta, tidak diketahui, atau kombinasi keduanya.
Cara Mengidentifikasi Trinomial Kuadrat Sempurna
Sekarang Anda tahu secara teori apa itu trinomial kuadrat sempurna, tetapi bagaimana Anda tahu jika trinomial spesifik yang Anda kerjakan adalah satu? Ingat, Anda tidak akan mendapatkan apa yang ada di sisi kanan tanda sama dengan dalam persamaan di atas. Itulah yang Anda coba temukan.
Untuk mengetahui apakah trinomial yang Anda kerjakan adalah trinomial kuadrat sempurna, Anda perlu memeriksa tiga kondisi berikut:
Kondisi 1: Suku pertama dan ketiga harus positif.
Kondisi 2: Suku pertama dan ketiga harus kuadrat sempurna.
Kondisi 3: Jika suku kedua positif , sama dengan 2 kali akar kuadrat suku pertama dan ketiga. Jika suku kedua negatif , hasilnya sama dengan -2 kali akar kuadrat suku pertama dan ketiga.
Anda memiliki trinomial kuadrat sempurna jika dan hanya jika ketiga syarat terpenuhi.
soal latihan
Cara terbaik untuk membiasakan diri bekerja dengan trinomial kuadrat sempurna adalah dengan mengerjakan soal latihan. Mari kita faktorkan sepasang trinomial bersama-sama.
masalah satu
Kita akan mulai dengan memeriksa daftar periksa untuk melihat apakah trinomial berikut adalah trinomial kuadrat sempurna.
|
|
Kondisi 1: Apakah suku pertama dan ketiga positif? Suku pertama kita adalah 4 x ^ 2 dan suku ketiga adalah 25. Keduanya positif, sehingga syarat ini lolos.
Kondisi 2: Apakah suku pertama dan ketiga kuadrat sempurna? Untuk menentukan ini, kami mengambil akar kuadratnya. Jika mereka kuadrat sempurna, konstanta harus berakhir sebagai bilangan bulat dan eksponen dari yang tidak diketahui harus berakhir sebagai bilangan bulat juga.
|
|
Kedua istilah juga lulus tes ini. Jika trinomial ini ternyata merupakan trinomial kuadrat sempurna, 2 x akan menjadi a dan 5 akan menjadi b dari rumus untuk memfaktorkan trinomial kuadrat sempurna.
Kondisi 3: Apakah suku kedua sama dengan dua kali akar kuadrat suku pertama dan ketiga?
|
|
Trinomial kita sekarang telah melewati ketiga syarat tersebut. Jadi kita bisa menggunakan rumus untuk memfaktorkan trinomial kuadrat sempurna ke dalamnya.
Pertama, kita perlu memeriksa mana dari dua versi rumus yang akan kita gunakan. Hal ini tergantung pada apakah istilah kedua adalah positif atau negatif. Karena positif (20x), kami akan menggunakan rumus berikut:
|
|
Kita telah melihat bahwa untuk trinomial ini a = 2 x dan b = 5. Mengetahui hal ini, kita mendapatkan jawaban berikut untuk trinomial terfaktor penuh kita.
|
|
masalah dua
Untuk soal latihan kedua kita, mari kita lihat sesuatu yang sedikit lebih rumit.
|
|
Kita dapat segera melihat bahwa ini gagal dalam syarat pertama kita, karena suku pertama dan ketiga adalah negatif. Namun, Anda tidak boleh menyerah begitu cepat. Kita dapat mencoba memfaktorkan yang negatif dari persamaan.
|
|
Sekarang suku pertama dan ketiga dalam tanda kurung adalah positif. Kita dapat terus memeriksa apakah yang ada di dalam tanda kurung adalah trinomial kuadrat sempurna.
Kita dapat melihat bahwa trinomial juga gagal pada kondisi kedua karena akar kuadrat dari x ^3 tidak dapat disederhanakan. kita dapat memfaktorkan x karena berada di masing-masing suku.
|
|
Ketika kita periksa lagi apa yang ada di dalam tanda kurung, kita dapat melihat bahwa kondisi kedua sekarang lolos.
|
|
Moral dari cerita ini adalah bahwa setiap kali trinomial gagal dalam salah satu dari dua syarat pertama, Anda harus selalu memeriksa ulang untuk memastikan tidak ada elemen bersama di antara ketiga suku yang dapat difaktorkan.
Akhirnya, kita dapat melihat bahwa trinomial melewati syarat ketiga.
|
|
Karena suku kedua dari trinomial ini negatif, kita menggunakan bentuk kedua dari persamaan trinomial kuadrat sempurna untuk memfaktorkannya.
|
|
Ringkasan Pelajaran
Dalam kursus aljabar, satu hal yang akan Anda pelajari adalah trinomial faktor , yaitu polinomial yang memiliki tiga suku. Jenis trinomial khusus disebut trinomial kuadrat sempurna dan tersedia dalam dua bentuk berikut:
|
|
Komponen, a dan B , yang membentuk trinomial kuadrat sempurna dapat berupa konstanta, tidak diketahui, atau kombinasi keduanya.
Untuk menentukan apakah trinomial spesifik yang Anda kerjakan adalah trinomial kuadrat sempurna, ketiga kondisi berikut harus terpenuhi:
Kondisi 1: Suku pertama dan ketiga harus positif.
Kondisi 2: Suku pertama dan ketiga harus kuadrat sempurna.
Kondisi 3: Jika suku kedua positif, sama dengan 2 kali akar kuadrat suku pertama dan ketiga. Jika negatif, hasilnya sama dengan -2 kali akar kuadrat suku pertama dan ketiga.
Sebagai peringatan terakhir, bahkan ketika trinomial tampaknya gagal dalam salah satu dari dua syarat pertama, selalu periksa bahwa tidak ada elemen di antara ketiga suku trinomial Anda yang dapat difaktorkan agar berfungsi sebagai kuadrat sempurna. trinomial.