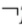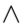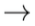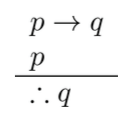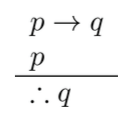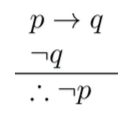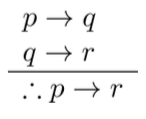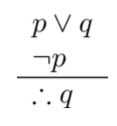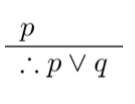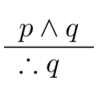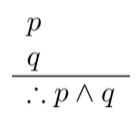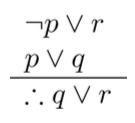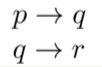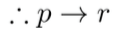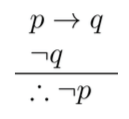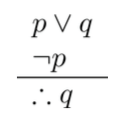Latar belakang
Hukum inferensi adalah aturan yang dapat dianggap sebagai alat utama untuk membangun argumen yang valid. Sebelum membahas apa itu hukum inferensi , mari kita ingat bahwa argumen adalah rangkaian pernyataan yang diakhiri dengan kesimpulan . Kami mengatakan bahwa argumen itu valid jika kesimpulannya mengikuti pernyataan sebelumnya. Perhatikan bahwa pernyataan di atas juga disebut premis .
Berikut adalah beberapa contoh argumen yang dibagi menjadi premis dan kesimpulannya.
- Plot: Jika matahari terbit, itu akan menjadi hari yang baik. Matahari telah terbit. Jadi ini akan menjadi hari yang baik.
Penduduk setempat: Jika matahari keluar, maka itu akan menjadi hari yang baik. Matahari telah terbit.
Kesimpulan: ini akan menjadi hari yang baik.
- Plot: Semua mobil berwarna merah atau biru. Mobil ini tidak berwarna merah. Oleh karena itu, mobil ini berwarna biru.
Tempat: Semua mobil berwarna merah atau biru. Mobil ini tidak berwarna merah.
Kesimpulan: Oleh karena itu, mobil ini berwarna biru.
- Plot: Saya akan tertawa. Oleh karena itu, saya akan tertawa atau menangis.
Premis: Saya akan tertawa.
Kesimpulan: Oleh karena itu, saya akan tertawa atau menangis.
Sekarang Anda sedikit lebih paham dengan struktur argumen. Penting untuk diketahui bahwa setiap argumen juga dapat direpresentasikan menggunakan variabel sebagai label untuk setiap pernyataan. Biasanya huruf p , q dan r digunakan. Selain itu, simbol digunakan untuk mengganti istilah logika utama:
Negasi (‘tidak’):
|
|
SALAH SATU:
|
|
Y:
|
|
Karena itu:
|
|
Jika kemudian:
|
|
Untuk memperjelas notasi ini, mari kita tulis ulang contoh pertama dalam bentuk variabel. Kami mulai dengan memberi label pada setiap pernyataan dengan huruf:
T: Matahari telah terbit.
T: Ini akan menjadi hari yang baik.
Sekarang mengganti variabel, kami memiliki:
Jika p, maka q . hal . Oleh karena itu , apa
Selanjutnya, kita akan mengganti istilah logika kunci dengan simbol yang sesuai dan menyusun variabel dalam format biasa untuk mewakili argumen lengkap. Perhatikan bahwa ini melibatkan meletakkan premis di atas satu sama lain, dan kemudian meletakkan kesimpulan di bawah garis. Berikut adalah argumen lengkap dalam format variabel:
|
|
hukum inferensi
Berikut adalah hukum inferensi dengan representasi variabel yang sesuai.
- Modus ponens
|
|
- Modus Tollens
|
|
- Silogisme hipotetis
|
|
- Silogisme disjungtif
|
|
- Tambahan
|
|
- Penyederhanaan
|
|
- Konjungsi
|
|
- Resolusi
|
|
Untuk membuat kesimpulan
Dengan menggunakan hukum inferensi, Anda juga dapat menarik kesimpulan berdasarkan premis yang Anda berikan. Mari kita lihat contoh cara kerjanya:
Misalkan Anda diberikan premis berikut: jika mendung, akan hujan. Jika hujan, tanah akan basah.
Untuk menarik kesimpulan berdasarkan premis-premis tersebut, kita mulai dengan mengubahnya menjadi simbol seperti yang ditunjukkan di atas.
T: Cuaca mendung.
T: Hujan.
J: Tanahnya basah.
|
|
Sekarang lihatlah hukum inferensi yang tercantum di atas. Yang memiliki premis yang sama?
Silogisme hipotetis benar! Jadi, berdasarkan hukum itu, kita tahu bahwa kesimpulannya pasti
|
|
Dengan kata lain: Oleh karena itu, jika mendung, maka tanah akan basah.
Bukti validitas argumen
Demikian pula, kita dapat menguji validitas argumen menggunakan hukum inferensi. Pertimbangkan argumen berikut:
- Plot: Jika hujan, maka rumputnya hijau. Rumputnya tidak hijau. Karena itu, hujan tidak turun.
Mengubah ini menjadi simbol yang kita miliki:
T: Hujan.
q: Rumputnya hijau.
|
|
Sekarang, melihat kembali hukum inferensi, kita melihat bahwa ini sama persis dengan hukum Modus Tollens. Oleh karena itu, kita dapat menyimpulkan bahwa argumen ini valid .
- Plot: Sekolah akan dibuka atau saya akan tinggal di rumah. Sekolah tidak dibuka. Oleh karena itu, saya tidak akan tinggal di rumah.
Mengubah ini menjadi simbol yang kita miliki:
T: Sekolah akan dibuka.
T: Saya akan tinggal di rumah.
Melihat kembali hukum inferensi, kita melihat bahwa premisnya sangat cocok dengan hukum silogisme disjungtif, tetapi kesimpulannya justru sebaliknya.
|
|
Kesimpulannya harus “Saya akan tinggal di rumah”. Oleh karena itu, argumen ini tidak valid .
Ringkasan Pelajaran
Singkatnya, ingatlah bahwa hukum inferensi adalah:
- Modus ponens
- Modus Tollens
- Silogisme hipotetis
- Silogisme disjungtif
- Penambahan
- Penyederhanaan
- Konjungsi
- Resolusi
Seperti yang telah kita lihat, mereka dapat digunakan untuk menarik kesimpulan berdasarkan premis yang diberikan, dan mereka juga dapat menguji validitas argumen.