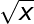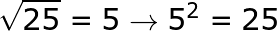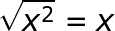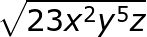Ikuti tanda-tandanya
Bagaimana jika Anda sedang mengemudi di jalan dan tiba-tiba semua orang memutuskan untuk mengabaikan rambu lalu lintas? Tidak ada yang berhenti di lampu merah, mengkhawatirkan sisi jalan mana yang mereka lalui atau bahkan berhenti untuk pejalan kaki. Itu akan menjadi kekacauan. Ada alasan mengapa tanda-tanda itu ada.
Bagaimana jika Anda berkendara ke kota berikutnya dan menemukan bahwa rambu lalu lintasnya berbeda dari biasanya? Mereka berhenti di lampu hijau, dan bukannya segitiga hasil, ada lingkaran ungu. Ada peraturan lalu lintas, tetapi Anda tidak tahu apa itu atau bagaimana mengikutinya. Itu sebabnya ada jenis marka jalan yang standar dan diterima untuk setiap keadaan.
Matematikanya sama. Ada tanda-tanda standar yang memberi tahu orang apa yang harus dilakukan dan tanda itu sama di mana-mana. Tidak ada kebingungan: ketika Anda melihat 8/2, Anda tahu untuk membagi, dan ketika Anda melihat 3 + 9, Anda tahu bahwa Anda harus menjumlahkan.
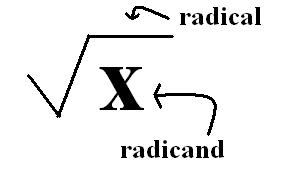
Apa itu radikal dan radikan?
Simbol yang menjadi perhatian kita dalam pelajaran ini adalah simbol radikal atau akar kuadrat. Simbol ini terlihat seperti ini:
|
|
dan memberi tahu Anda untuk menemukan angka yang jika dikalikan dengan dirinya sendiri sama dengan angka di bawah simbol akar. Angka di bawah simbol radikal itu disebut radicand .
|
|
Apa yang dimaksud dengan radikal dan radikan?
Saat Anda menyusuri jalur matematika, tanda jalan radikal ingin Anda mengambil akar kuadrat dari istilah di dalam simbol, atau radikan. Fungsi akar kuadrat adalah kebalikan atau kebalikan dari fungsi kuadrat. Saat Anda diminta untuk mengkuadratkan sebuah angka , Anda harus mengambil angka tersebut dan mengalikannya dengan angka itu sendiri.
Sebagai contoh:
|
|
Aturan yang sama berlaku untuk angka dan variabel.
|
|
Dalam ekspresi apa pun dengan simbol radikal, suku di bawah akar kuadrat adalah radikan, meskipun ekspresinya besar, seperti ini:
|
|
Dalam contoh ini, 23 x ^ 2 y ^ 5 z adalah radikan.
Ekspresi radikal dari bilangan real
Saat mempelajari radikal, kita harus memastikan bahwa kita bekerja dengan bilangan real.
Bilangan riil adalah bilangan apa pun yang tidak imajiner. Sebenarnya, itulah definisinya. Istilah “bilangan real” tidak diciptakan sampai bilangan imajiner ditemukan dan istilah diperlukan untuk menggambarkan semua bilangan lainnya.
Angka sebenarnya antara lain:
- Bilangan bulat: 0, 1, 2, 3 …
- Bilangan rasional: contohnya termasuk 3/4, 0,125, 0,333
- Bilangan irasional, seperti pi dan akar kuadrat dari 3
Bilangan real tidak termasuk akar kuadrat dari negatif 1, tak terhingga, dan beberapa hal lain yang digunakan matematikawan dalam matematika tingkat sangat tinggi.
Apakah suku-suku berikut mewakili bilangan real?
- 64
- 5
- 1.7
- 3.26
- -4
- -7.8
Semua contoh ini terlihat seperti bilangan real apa adanya, tetapi sesuatu terjadi ketika Anda mencoba mengambil akar kuadrat dari bilangan negatif. Tidak Menghitung. Itu karena akar kuadrat dari minus 1 adalah imajiner. Jadi masuk akal bahwa akar kuadrat dari bilangan negatif apa pun tidak terdefinisi. Ini karena angka negatif apa pun dapat difaktorkan menjadi pasangan positif dan negatifnya, seperti:
-4 = (4) * (-1)
-7,8 = (7,8) * (-1)
…Karena akar kuadrat dari angka negatif apa pun dapat didekomposisi menjadi akar kuadrat dari angka positif yang dikalikan dengan akar kuadrat dari 1. Dan 1 negatif itu membuat ekspresi radikal negatif apa pun menjadi imajiner.
Ringkasan Pelajaran
Radikal adalah ekspresi dengan simbol akar kuadrat. Istilah di bawah simbol akar kuadrat disebut radikan. Radicand dapat berupa angka atau variabel. Agar ekspresi radikal menjadi nyata, ia tidak boleh negatif, karena akar kuadrat dari negatif 1 adalah imajiner dan oleh karena itu tidak terdefinisi.
hasil pembelajaran
Setelah meninjau pelajaran ini, Anda akan memiliki kemampuan untuk:
- Definisi radikal dan radikal
- Jelaskan fungsi akar kuadrat dan fungsi kuadrat.
- Jelaskan mengapa ekspresi radikal tidak boleh negatif.