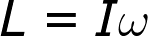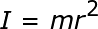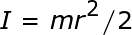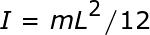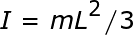Momentum sudut: persamaan dasar
Untuk momentum linier, kita menggunakan persamaan P = mv , di mana P adalah momentum, m adalah massa dalam kilogram, dan v adalah kecepatan dalam meter per detik. Persamaan momentum sudutnya adalah:
|
|
di mana L adalah momentum sudut, I adalah momen inersia, dan omega adalah kecepatan sudut. Kecepatan sudut dapat dikaitkan dengan kecepatan linier, v , jika Anda mengetahui jari-jarinya, r , dari pusat rotasi menggunakan persamaan w = v/r . Namun, momen inersia suatu benda ditentukan oleh tiga faktor: massa, bentuk, dan sumbu rotasinya.
Contoh momen inersia
Momen inersia I massa titik yang bergerak melingkar dengan jari-jari r :
|
|
Momen inersia piringan:
|
|
Momen inersia batang tipis terhadap pusatnya:
|
|
Momen inersia batang tipis pada ujungnya:
|
|
masalah titik massa
Jenis masalah momentum sudut yang paling mudah adalah yang melibatkan massa titik , atau partikel titik yang berputar di sekitar pusat sumbu. Contoh masalah massa titik dapat berupa apa saja, mulai dari bola di tali hingga benda seukuran planet. Dengan menggunakan persamaan momentum dan mensubstitusikan momen inersia massa titik berotasi, kita mendapatkan L = mrv . Jadi soal-soal ini bergantung pada massa, jari-jari, dan kecepatan linier.
masalah 1
Berapa momentum sudut penangkap bola bisbol yang dilempar dengan kecepatan 40 m/s? Berat bola adalah 145 kilogram dan di lapangan liar penangkap menjulurkan lengannya sejauh 1,25 m dari pusat putarannya.
L = mrv
L = (0,145kg)(1,25m)(40m/dtk)
L = 7,25kg/m2/detik
masalah 2
Sebuah bola berputar pada tali 5 ft dari ujung pipa berongga dengan kecepatan linier 10 ft/s. Tali terus menuruni pipa ke ujung lainnya. Berapa kecepatan linier baru bola jika Anda menarik tali sejauh 3 kaki, sehingga memperpendek jari-jari girasi bola?
Karena momentum kekal antara dua keadaan (selama kita mengabaikan gesekan, berat tali, dan diameter pipa), momentum sudut yang baru dan momentum sudut yang lama akan sama.
L (lama) = L (baru)
mrv (lama) = mrv (baru)
m (5)(10) = m (5-3)( v )
Massa batal berangkat:
50 = 2v
v = 25 kaki/dtk
masalah 3
Apakah kecepatan linier Bumi meningkat saat bergerak dari jarak terjauh dari matahari ke jarak terdekatnya? Perihelion (saat Bumi paling dekat dengan Matahari) = 91,4 juta mil dan Aphelion (saat Bumi paling jauh dari Matahari) = 94,5 juta mil.
Meskipun kelihatannya seperti masalah yang sangat berbeda, kita dapat menggunakan pendekatan yang sama dengan masalah ball-on-string di atas.
L (lambat) = L (cepat)
mrv (lambat) = mrv (cepat)
m (94,5)( v ) = m (91,4)( v )
Massa dibatalkan, yang berarti bahwa persentase peningkatan kecepatan hanya ditentukan oleh perubahan jari-jari perihelion dan aphelion.
% peningkatan kecepatan = (94,5 – 91,4) / 91,4 = 3,4%
Memutar Masalah Silinder Padat
Masalah silinder akhirnya menjadi sangat mirip dengan masalah massa titik karena momen inersia piringan yang berputar di sekitar pusatnya adalah setengah dari momen massa titik yang berputar dengan jari-jari yang sama. Dalam bentuk persamaan, momentum sistem jenis ini menjadi:
L = mrv / 2
Titik A pada keliling piringan bergerak dengan kecepatan 10 m/s. Jika dua piringan kembar dengan bahan dan ketebalan yang sama, tetapi tanpa rotasi, diletakkan di atas piringan pertama, berapa kecepatan linier akhir titik A?
L (lama) = L (baru)
mrv /2 = mrv /2
Tetapi bagaimana jika massa baru tiga kali massa lama, dan kecepatan lama 10 m/s?
mr (10) / 2 = 3 mrv / 2
Kita melihat bahwa m dan r keduanya lenyap, meninggalkan:
5 = 1,5 ( v )
V = 5 / 1,5 = 3,33 m / s.
Ringkasan Pelajaran
Semua masalah momentum sudut dimulai dengan persamaan ini:
|
|
Persamaan ini dibaca sebagai momentum sudut sama dengan momen inersia dikalikan dengan omega, atau kecepatan sudut.
Trik untuk memecahkan masalah momentum sudut adalah dengan mengatur persamaan menggunakan bentuk rotasi dan sumbu rotasi yang benar.