Jenis transformasi
Halo dan selamat datang di pelajaran tentang transformasi dasar grafik polinomial ini. Untuk memulainya, mungkin ada baiknya untuk mengetahui apa itu polinomial dan seperti apa bentuk grafik polinomial dasarnya.
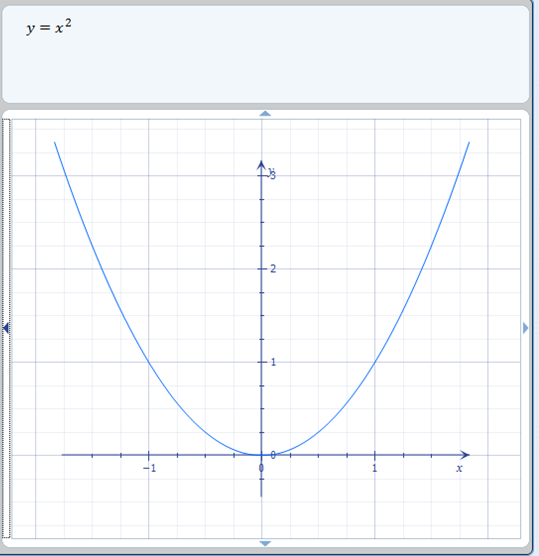
Nah, polinomial adalah kependekan dari fungsi polinomial , dan itu mengacu pada fungsi aljabar yang dapat memiliki banyak suku. Biasanya disajikan dengan notasi f dari x seperti ini: f ( x ) = x ^ 2.
f ( x ) = x ^ 2 adalah fungsi induk karena merupakan fungsi satuan standar dari bentuk tersebut. Grafik terlihat seperti parabola halus dengan kedua ujungnya berada di atas sumbu x , dan grafik melewati titik (1,1) dan (-1, 1).
|
|
|
grafik polinomial |
Apa yang Anda pikirkan ketika mendengar kata ‘transformasi’? Saya biasanya memikirkan sesuatu yang berubah. Mungkin warna merah, berubah atau berubah menjadi warna jingga bila ditambahkan kuning. Atau siapa yang bisa melupakan mobil klasik menjadi transformasi robot? Segala jenis perubahan dari satu hal atau tampilan ke hal lain dapat dianggap sebagai transformasi.
Pelajaran ini berfokus pada transformasi grafik polinomial , yang, secara sederhana, mengubah grafik fungsi polinomial. Untuk pembahasan yang lebih mendalam tentang grafik polinomial, lihat pelajaran tentang memahami grafik polinomial.
Jadi, kembali ke gambar graf induk dasar dari f ( x ) = x ^2, transformasi apa saja yang dapat dilakukan oleh graf ini? Itu bisa bergerak ke atas dan ke bawah, ke kiri dan ke kanan; itu bisa terjepit atau meregang, atau bahkan bisa terbalik. Mari kita lihat bagaimana mencapai masing-masing jenis transformasi ini secara terpisah, lalu kita akan menyimpulkan dengan menggabungkannya menjadi satu transformasi besar.
transformasi atas dan bawah
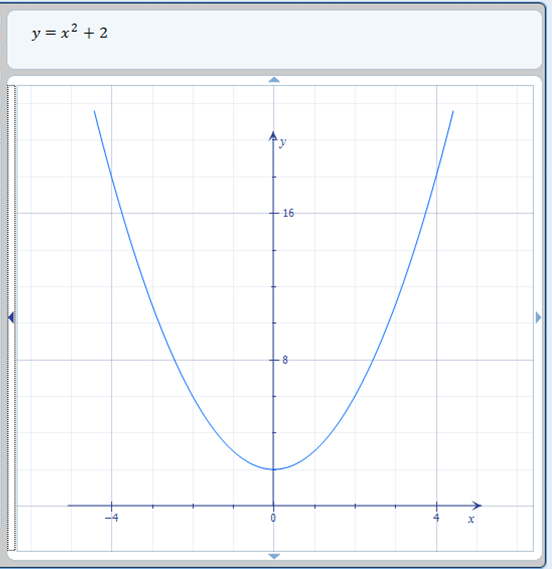
Transformasi naik dan turun untuk fungsi disebabkan oleh penambahan atau pengurangan angka di luar fungsi aslinya. Oleh karena itu, f ( x ) + 2 akan memindahkan grafik ke atas 2 tempat. Dalam contoh kita, kita menggunakan fungsi induk dari f ( x ) = x ^ 2, jadi untuk menaikkannya, kita akan membuat grafik f ( x ) = x ^ 2 + 2.
|
|
|
transformasi di atas |
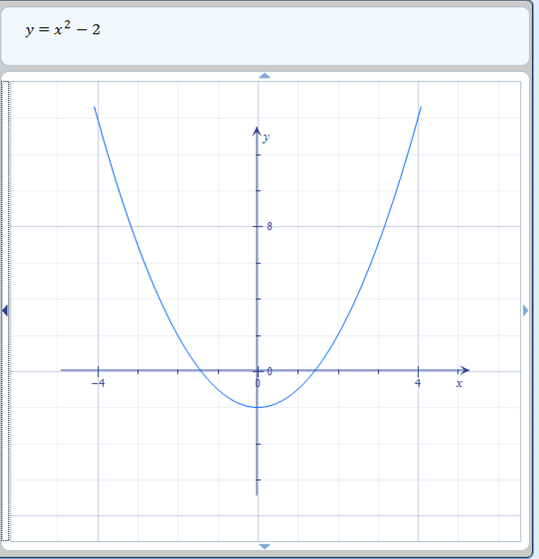
Memindahkan grafik ke bawah adalah prinsip yang sama, kecuali kita mengurangi. f ( x ) = x ^ 2 – 2 memindahkan grafik utama turun dua tempat. Perhatikan bagaimana titik belok pada bagan berada di -2 pada bagan yang diubah alih-alih nol seperti pada bagan utama.
|
|
|
transformasi bawah |
Jadi bergerak naik turun membutuhkan penambahan atau pengurangan (masing-masing) di luar fungsi. Ini adalah transformasi termudah karena masuk akal secara logis: ketika Anda menambahkan, Anda menambah (atau naik); ketika Anda mengurangi, Anda mengurangi (atau turun).
transformasi kiri dan kanan
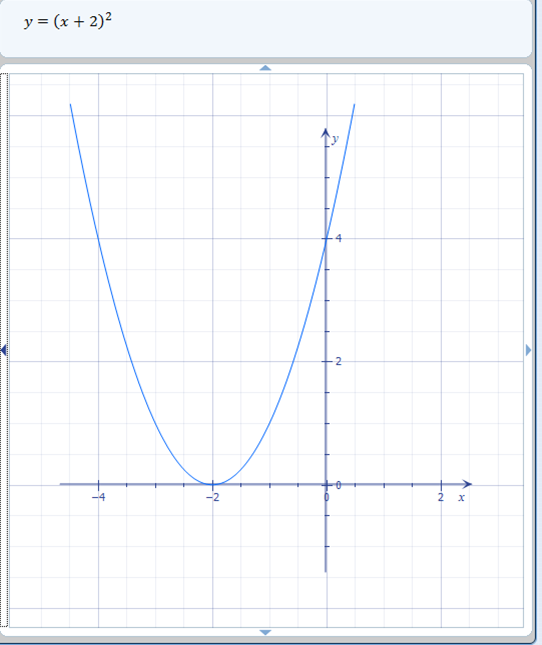
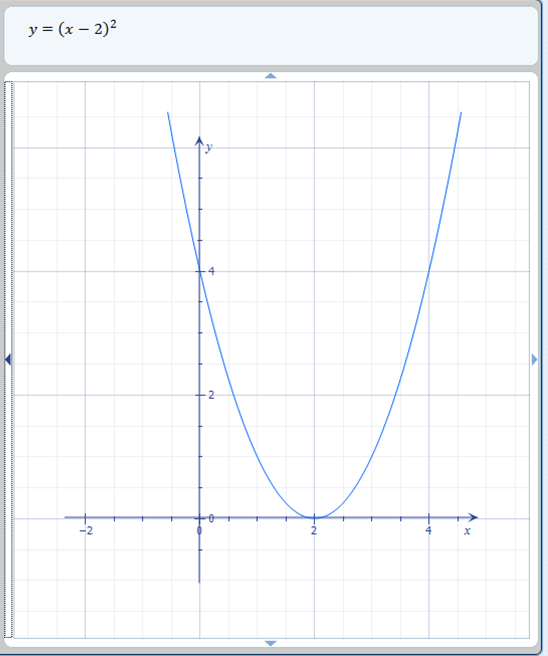
Untuk bergerak ke kiri dan ke kanan, kita harus menjumlahkan atau mengurangi di dalam fungsi seperti ini: f ( x + 2) = ( x + 2) ^ 2. Pindah ke atas dan ke bawah itu logis. Bergerak ke kiri dan ke kanan sebenarnya kebalikan dari apa yang logis. Jika Anda menambahkan 2 ke fungsi, Anda benar-benar memindahkan grafik kembali ke kiri 2 tempat.
|
|
|
transformasi ke kiri |
Berpikir secara matematis, logikanya tetap ada, justru sebaliknya. Ingat, untuk membuat grafik dengan tangan, kita selalu mencari nilai yang sama dengan y jika x adalah nilai yang diberikan. Biasanya, kita mencoba mencari tahu x apa yang kita butuhkan untuk membuat y = 0. Jika fungsi Anda adalah f ( x ) = ( x + 2) ^ 2, sebenarnya cukup mudah untuk melihat bahwa kita membutuhkan x = -2 untuk y menjadi 0. Jadi, x = -2 jelas akan memindahkan grafik ke kiri. Jadi sementara pada awalnya tampak tidak masuk akal bahwa fungsi add inside akan bergerak ke kiri, ketika Anda melihat lebih dekat, itu jelas benar.
Kebalikannya juga benar. f ( x – 2) = ( x – 2)^2 artinya kita membutuhkan x positif 2 agar y menjadi 0. Ini akan memindahkan grafik ke kanan (ke arah positif untuk sumbu x ).
|
|
|
Hak transformasi |
Saat bergerak ke kiri dan ke kanan, penambahan atau pengurangan dilakukan di dalam fungsi, dan gerakannya adalah logika terbalik (penjumlahan bergerak ke kiri, pengurangan bergerak ke kanan).
cubit dan regangkan
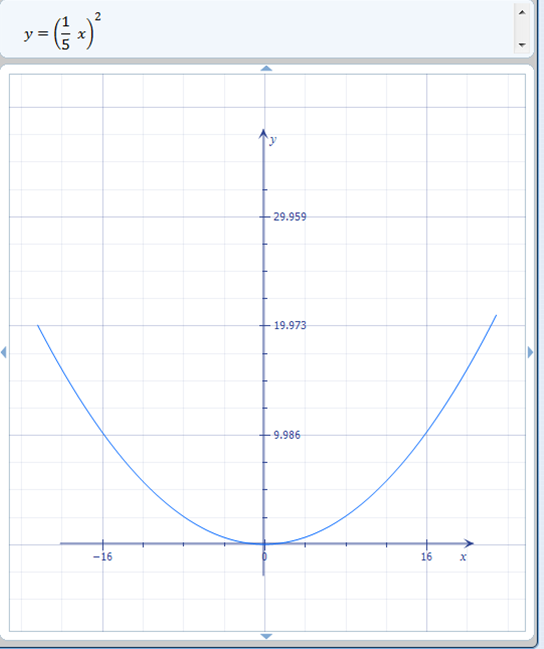
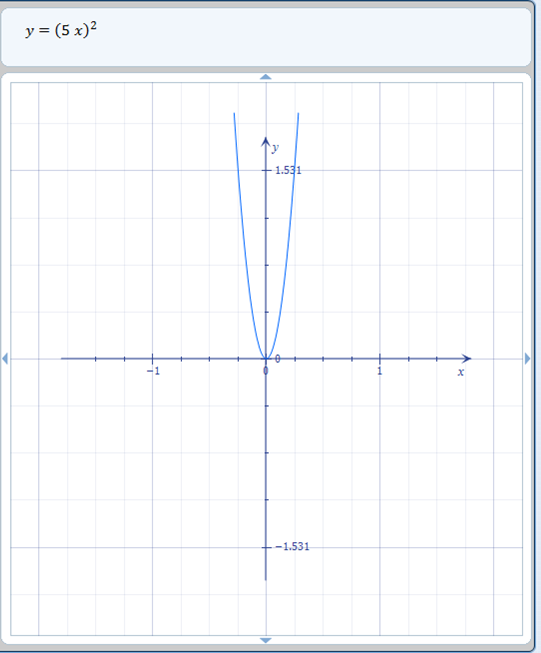
Kami sekarang beralih ke mengalikan fungsi. Transformasi ini bergantung pada apakah pengalinya lebih besar atau lebih kecil dari 1: pengali yang kurang dari 1 meregangkan grafik, sedangkan pengali yang lebih besar dari 1 mencubit grafik. Masuk akal logis bahwa mengalikan suatu fungsi dengan pecahan (kurang dari 1) akan melebarkan grafik karena setiap nilai y yang dihasilkan hanyalah sebagian kecil dari nilai x yang dipilih .
|
|
|
Perpanjangan |
Demikian pula, karena mengalikan dengan bilangan bulat lebih besar dari 1 akan meningkatkan hasil y dalam fungsi apa pun, mudah untuk melihat bahwa ini akan mengurangi grafik fungsi utama (nilai y meningkat lebih cepat daripada nilai x karena pengali ) . Mengalikan dengan angka yang kurang dari 1 akan meregangkan grafik, seperti halnya angka yang lebih besar dari 1 akan memperkecil grafik.
|
|
|
Pencurian |
flip chart
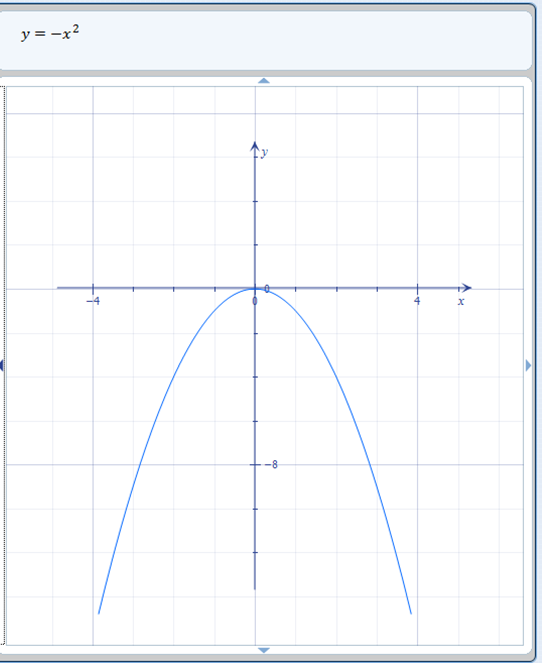
Bentuk transformasi terakhir adalah twist. Saat Anda membalik bagan, pada dasarnya Anda menampilkan bentuk kebalikan dari bagan itu. Apa lawan kata dalam aljabar? Itu benar, negatif! Jadi yang harus Anda lakukan untuk membalik grafik adalah membuatnya negatif.
Contoh fungsi induk kita adalah f ( x ) = x ^ 2, jadi kebalikannya (atau negatif) versinya adalah f ( x ) = – x ^ 2 dan inilah transformasinya:
|
|
|
Balik |
Untuk membalikkan grafik, yang harus Anda lakukan adalah membuat fungsinya menjadi negatif.
Contoh Transformasi
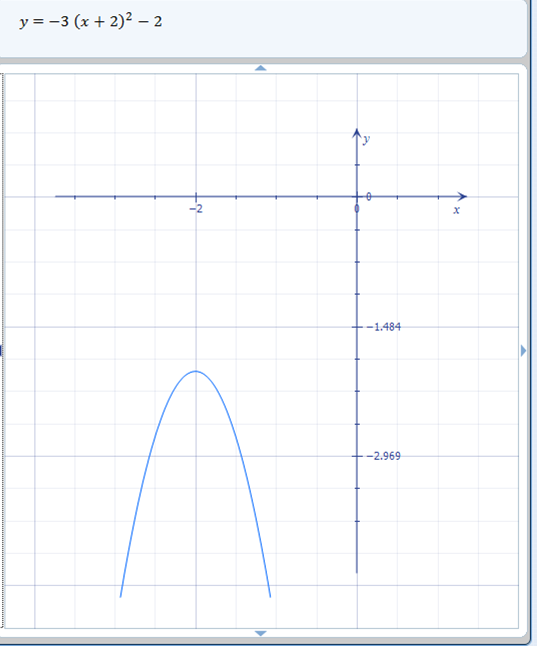
Jadi bagaimana jika kita menempatkan semua transformasi ini dalam satu grafik? Bagaimana bentuk grafik dari f ( x ) = -3 ( x + 2) ^ 2 – 2? Baiklah, pertama mari kita tinjau fungsinya:
- Kami memiliki -2 di luar fungsi, jadi kami akan turun dua tempat.
- Ada penambahan 2 di dalam fungsi, sehingga grafik akan berpindah dua tempat ke kiri.
- Ada bilangan bulat pengali 3, sehingga grafik akan berkurang.
- Ini negatif, sehingga seluruh grafik akan terbalik.
|
|
|
Contoh Transformasi |
Dan begitulah, grafik berubah persis seperti yang kami perkirakan. Jangan lupa bahwa aturan ini berlaku untuk semua fungsi polinomial, bukan hanya f ( x ) = x ^ 2.
Ringkasan Pelajaran
Dalam pelajaran ini, kita membahas empat jenis transformasi graf polinomial. Fungsi utama yang paling dasar digunakan untuk mengilustrasikan transformasi. Sebagai ulasan:
- Transformasi naik dan turun terjadi saat penjumlahan atau pengurangan di luar fungsi.
- Transformasi kiri dan kanan terjadi saat menambah atau mengurangi di dalam fungsi.
- Grafik mencubit saat dikalikan dengan angka yang lebih besar dari 1 dan membentang saat dikalikan dengan angka yang lebih kecil dari 1.
- Untuk membalikkan grafik, buat fungsi negatif.
Mempelajari keempat transformasi ini akan membantu Anda menganalisis grafik polinomial apa pun yang Anda lihat. Terima kasih telah bergabung dengan saya.
hasil pembelajaran
Selama pelajaran ini, Anda dapat mengembangkan kemampuan untuk:
- Tentukan polinomial dan fungsi induk
- Buat empat transformasi: atas/bawah, kiri/kanan, cubit/regangkan, dan balik