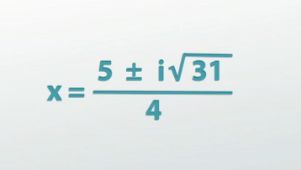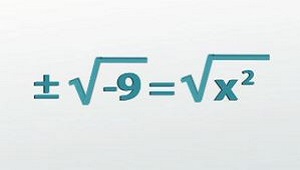Cara menyelesaikan kuadrat dengan bilangan kompleks sebagai solusi =>

Bilangan imajiner dan kompleks

Dengan membiarkan diri kita membayangkan bahwa ada akar kuadrat dari bilangan negatif, kita dapat menyelesaikan banyak masalah dunia nyata. Jadi seperti apa sebenarnya itu? Bagaimana Anda memecahkan masalah yang memiliki solusi imajiner? Tentang itulah pelajaran ini.

Anda harus ingat bahwa bilangan imajiner adalah saat kita mengambil akar kuadrat dari bilangan negatif, dan bilangan kompleks adalah saat kita menggabungkan bilangan real dengan bilangan imajiner dengan menambahkan atau mengurangi. Jika ini adalah konsep baru bagi Anda, maka Anda harus meninjau pelajaran sebelumnya yang memperkenalkan ide-ide ini, tetapi jika Anda sudah mengetahuinya, kami siap untuk melihat ‘mencari akar y = 2 x ^ 2 – 5 x + 7. ‘ contoh.

Kuadrat dengan solusi kompleks

Ketika sebuah soal meminta akar, itu sama dengan menanyakan nol atau x -intercepts . Ini adalah titik di mana y = 0, jadi kita bisa memasukkan nilai itu untuk memulai.

Mengingat fakta bahwa kita melakukan contoh ini dalam pelajaran tentang memecahkan bilangan kompleks, kemungkinan besar inilah yang akan terjadi pada masalah ini. Tapi bagaimana kita bisa tahu ini jika masalah ini tidak ada dalam konteks ini?

Itu semua akan bermuara pada yang diskriminan. Diketahui persamaan kuadrat dalam bentuk standar ( y = ax ^ 2 + bx + c ) , diskriminannya adalah b ^ 2 – 4 ac . Jika diskriminan positif, Anda akan mendapatkan dua jawaban nyata. Jika sama dengan nol, Anda hanya akan mendapatkan jawaban yang sebenarnya. Tetapi jika diskriminan negatif, saat itulah Anda mendapatkan dua solusi kompleks untuk masalah Anda.

Ini terjadi karena cara kerja rumus kuadrat. Jika kita mulai menyelesaikan contoh menggunakan rumus kuadrat, seperti yang ditunjukkan di sini, Anda mungkin memperhatikan bahwa diskriminan adalah bagian dari rumus yang ada di dalam akar kuadrat. Jadi masuk akal jika bagian itu negatif, kita akan mendapatkan bilangan imajiner di sana, membuat jawaban kita menjadi bilangan kompleks.

Jadi, kembali ke contoh kita, jika kita memasukkan a , b , dan c ke dalam rumus dan kemudian mulai mengevaluasi ekspresi, kita akan menemukan bahwa diskriminan akan menjadi negatif. Anda akan melihat bahwa kita berakhir dengan akar kuadrat dari -31, yang akan menjadi bilangan imajiner. Meskipun inilah yang membuat masalah ini baru dan berbeda, satu-satunya hal khusus yang harus dilakukan adalah meletakkan i di depan akar kuadrat untuk menunjukkan bahwa itu imajiner, jadikan semua yang lain di dalam akar kuadrat positif dan kemudian lanjutkan seperti biasa. Itu dia! Saya memberi tahu semua orang bahwa ini adalah angka imajiner, tetapi kemudian kita dapat melanjutkan dan melanjutkan menyelesaikan masalah seperti biasa.

Ternyata tidak ada hubungannya dengan masalah ini; itu sesederhana mungkin. Mungkin jika kita dapat menyederhanakan akar kuadrat, kita dapat memiliki beberapa langkah lagi, tetapi kita tidak dapat melakukannya, jadi selesai!

Polinomial dengan solusi kompleks

Kita juga dapat menyelesaikan masalah polinomial dengan solusi imajiner yang lebih besar dari persamaan kuadrat. Ambil contoh ini: Selesaikan 0 = ( x – 9) ^ 2 * ( x ^ 2 + 9).

Ini bukan lagi persamaan kuadrat karena ada dua x ^2 (di sini dan di sini). Kami tidak memiliki rumus elegan untuk masalah seperti yang kami lakukan untuk kuadrat, tetapi karena cara penulisannya, kami masih bisa menyelesaikannya.

Kami akan menggunakan properti zero product untuk yang satu ini. Itu adalah sifat yang menyatakan bahwa setiap kali Anda mengalikan dua hal dan mendapatkan nol, salah satu hal yang Anda kalikan di awal pasti nol. Dalam soal ini, artinya ( x – 9) ^ 2 atau ( x ^ 2 + 9) harus nol. Sekarang setelah kita membagi persamaannya, kita memiliki dua persamaan yang lebih kecil yang kita tahu cara menyelesaikannya secara sederhana dengan operasi invers.

Mendapatkan x dengan sendirinya dalam yang pertama ini berarti membatalkan pangkat 2 dengan akar kuadrat. Akar kuadrat dari nol masih nol, sehingga meninggalkan kita di sini. Sekarang membatalkan -9 dengan +9 memberi tahu kita bahwa x = 9.

Pindah ke persamaan lain mengharuskan kita untuk membatalkan langkah serupa, hanya dalam urutan yang berbeda. Hal terluar di sini adalah +9, jadi kita perlu membatalkannya terlebih dahulu. Itu menyisakan x ^2 = -9, dan sekali lagi kita mengambil akar kuadrat dari kedua sisi untuk mendapatkan x itu sendiri. Saat kita mengambil akar kuadrat dari bilangan bukan nol, kita perlu menyertakan akar positif dan negatif, yang memberi kita dua jawaban di sini.

Kami juga mengambil akar kuadrat dari angka negatif, yang berarti kami juga memiliki solusi imajiner. Itu berarti meletakkan i di depan akar kuadrat dan melanjutkan seperti biasa, seperti sebelumnya. Kali ini kita bisa melangkah lebih jauh karena akar kuadrat dari 9 hanya 3. Jadi, dua penyelesaian kita yang lain di sini positif dan negatif 3 i .

Meskipun video ini tentang menyelesaikan soal dengan bilangan kompleks, karena yang harus Anda lakukan hanyalah menjumlahkan i dan melanjutkan seperti biasa, ini lebih merupakan ulasan keterampilan penyelesaian sebelumnya. Selama Anda mengingat hal ini dan tidak menganggap bilangan kompleks mengharuskan Anda melakukan sesuatu yang sangat radikal, Anda harus menjadi baik.

Ringkasan Pelajaran

Untuk meninjau: Diskriminan ( b ^ 2 – 4 ac ) akan memberi tahu Anda apakah Anda memiliki solusi nyata atau kompleks untuk persamaan kuadrat dalam bentuk standar. Saat Anda perlu mengambil akar kuadrat dari angka negatif, cukup letakkan i di depannya, jadikan angka di dalamnya positif, dan lanjutkan seperti biasa. Anda dapat menyelesaikan soal polinomial orde tinggi menggunakan properti hasil kali nol , yang menyatakan bahwa saat Anda mengalikan dua benda dan mendapatkan nol, salah satu benda yang Anda mulai harus nol.

Tujuan Pelajaran

Setelah Anda menyelesaikan pelajaran ini, Anda akan dapat:

• Gunakan diskriminan untuk mengetahui apakah Anda memiliki solusi nyata atau kompleks untuk persamaan kuadrat.
• Ambil akar kuadrat dari bilangan negatif
• Selesaikan masalah polinomial orde tinggi menggunakan properti produk nol