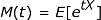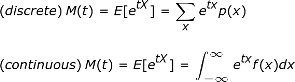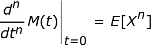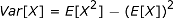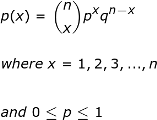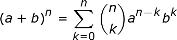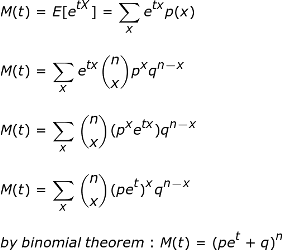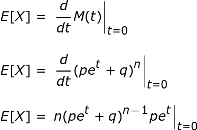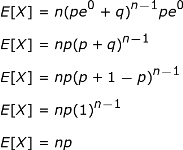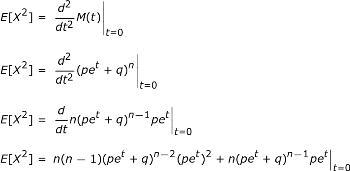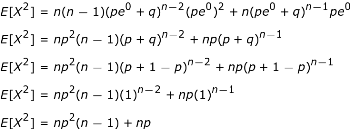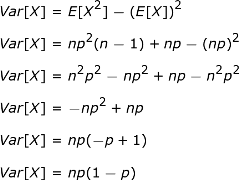momen
Saat mempelajari variabel acak dan distribusi probabilitasnya, beberapa konsep pertama yang dipelajari siswa statistik adalah nilai dan varian yang diharapkan. Nilai atau rata-rata yang diharapkan dari variabel acak ( X ) adalah rata-ratanya, dan varians adalah sebaran distribusi probabilitas.
Nilai yang diharapkan dan varians adalah contoh besaran yang dikenal sebagai momen, di mana momen digunakan untuk melakukan pengukuran tentang kecenderungan sentral dari sekumpulan nilai. Kita dapat menemukan momen distribusi probabilitas menggunakan fungsi pembangkit momennya. Dalam pelajaran ini, kita akan mempelajari cara menemukan fungsi penghasil momen, serta cara menggunakannya untuk menemukan nilai dan varians yang diharapkan.
Fungsi pembangkit momen
Fungsi penghasil momen , atau MGF, seperti namanya, adalah fungsi yang digunakan untuk menemukan momen dari variabel acak yang diberikan. Rumus untuk mencari FGM (M ( t )) adalah sebagai berikut, di mana E adalah nilai yang diharapkan:
|
|
Ini adalah rumus umum untuk mencari FGM dengan syarat ada bilangan positif b , sehingga b ≤ | t |. Cara menghitungnya dalam praktiknya berbeda tergantung pada apakah kita bekerja dengan distribusi probabilitas diskrit atau kontinu.
|
|
Dalam persamaan ini, p( x ) dan f( x ) adalah fungsi kerapatan dari distribusi probabilitas yang diberikan.
Temukan nilai yang diharapkan dan varians
Begitu kita memiliki FGM, kita perlu tahu cara menggunakannya untuk menghasilkan momen. Kami melakukan ini dengan mengambil turunan FGM dan mengevaluasinya pada t sama dengan 0.
|
|
Setiap turunan FGM yang berurutan memberi Anda momen yang berbeda. Setiap momen sama dengan nilai ekspektasi X yang dipangkatkan dengan bilangan momen tersebut.
Dengan mengambil turunan pertama ( n = 1) dari FGM dan menyetel t sama dengan 0, kami menemukan nilai harapan atau rata-rata dari variabel acak X . Turunan kedua ( n = 2) memberi kita nilai harapan dari X 2 , yang dapat digunakan untuk mencari varians dengan rumus berikut:
|
|
contoh soal
Untuk memahami sepenuhnya bagaimana kita menggunakan FGM, mari kita selesaikan beberapa masalah bersama. Untuk masalah pertama kita, kita akan menemukan FGM untuk distribusi probabilitas yang diketahui. Dalam hal ini, mari cari FGM dari distribusi binomial. Jika Anda membutuhkan pengingat cepat, distribusi binomial adalah distribusi probabilitas diskrit, dan fungsi kerapatannya diberikan di bawah ini, di mana p adalah probabilitas keberhasilan dan q = 1 – p :
|
|
Untuk menemukan FGM ini, kita harus bekerja dengan memanipulasi deret yang dilambangkan dengan tanda plus (∑), seperti yang harus Anda lakukan saat menemukan FGM dari distribusi probabilitas diskrit. Jika Anda agak bingung berurusan dengan ini, mungkin ada baiknya Anda meninjau beberapa cara umum kita bekerja dengan deret di kelas matematika, seperti deret Taylor atau teorema binomial. Faktanya, kita membutuhkan teorema binomial untuk dapat menyelesaikan masalah ini.
|
|
Dengan dua informasi ini, kami memiliki semua yang kami butuhkan untuk menemukan FGM dari distribusi binomial.
|
|
Sekarang setelah kita menemukan FGM dari distribusi binomial, mari kita gunakan untuk menemukan nilai dan varians yang diharapkan untuk contoh soal kedua kita.
Untuk nilai yang diharapkan, yang secara khusus kita cari adalah nilai yang diharapkan dari variabel acak X . Untuk menemukannya, kita mulai dengan mengambil turunan pertama FGM.
|
|
Setelah kita menemukan turunan pertama, kita mencari nilai harapan dari X dengan menyetel t sama dengan 0.
|
|
Kami sekarang beralih untuk menemukan varians. Kita ingin memulai dengan mencari nilai harapan dari X 2 . Untuk melakukan ini, kita perlu menemukan turunan kedua dari FGM.
|
|
Selanjutnya, kita sekali lagi menetapkan t sama dengan 0.
|
|
Nah, apa yang kita temukan di sini bukanlah variasi. Untuk menemukannya, kami menggunakan rumus varians kami, yaitu nilai harapan dari X 2 (yang baru saja kami temukan) dikurangi kuadrat dari nilai harapan X (yang kami temukan sebelumnya).
|
|
Ringkasan Pelajaran
Mari luangkan beberapa menit untuk mengulas apa yang telah kita pelajari!
Dalam statistik, kita sering mendapati diri kita bekerja dengan nilai dan varian yang diharapkan (rata-rata). Keduanya adalah contoh jenis kuantitas yang dikenal sebagai momentum , yang digunakan untuk mengukur kecenderungan sentral dari sekumpulan nilai.
Baik nilai yang diharapkan maupun varians merupakan besaran penting dalam statistik, dan kita dapat menemukannya menggunakan fungsi pembangkit momen (MGF), yang menemukan momen dari distribusi probabilitas tertentu. Jika kita mengetahui distribusi probabilitas (p( x ) dan f( x )) dalam pertanyaan, kita dapat mencari FGM(M( t )) menggunakan rumus berikut:
|
|
Setelah Anda memiliki FGM, temukan momen dari distribusi probabilitas dengan mengambil turunannya dan menetapkan t sama dengan nol.
|
|
Momen pertama ( n = 1) menemukan nilai harapan atau mean dari variabel acak X . Momen kedua ( n = 2) menemukan nilai harapan dari X 2 . Terakhir, kita dapat menggunakan keduanya untuk mencari varians menggunakan rumus berikut:
|
|