Simetri
Anda mungkin sering melihat simetri dalam kehidupan nyata. Setiap kali Anda bercermin, kaca, dan bahkan air, Anda dapat melihat pantulan diri Anda sendiri. Ini disebut simetri. Simetri dibuat ketika ada replika atau refleksi yang tepat dari suatu bentuk atau garis. Anda juga dapat melihat simetri pada objek sehari-hari. Misalnya, Anda dapat mengambil sebuah cangkir dan membayangkan sebuah garis di tengah cangkir itu. Di setiap sisi garis itu, cangkir itu memiliki replika atau pantulan yang tepat dari dirinya sendiri.
Bunga juga sering memiliki simetri.
|
Garis simetri menciptakan dua sisi yang sama |
Ada beberapa bentuk yang simetris hanya jika Anda menggambar garis di tempat yang tepat. Lihatlah pensil ini.
Dalam matematika, kita akan menyebut garis horizontal pada pensil itu sebagai sumbu atau garis simetri. Kami menyebutnya demikian karena garis itulah yang menunjukkan pantulan pensil; tidak ada garis lain yang akan menciptakan pantulan pada pensil.
Apa itu sumbu simetri?
Sumbu atau garis simetri adalah garis imajiner yang melewati pusat garis atau bentuk yang menciptakan dua bagian yang sangat identik. Dalam matematika tingkat yang lebih tinggi, Anda akan diminta untuk menemukan garis simetri parabola.
Ini adalah parabola , garis berbentuk U pada grafik.
|
|
Identifikasi garis simetri secara grafis
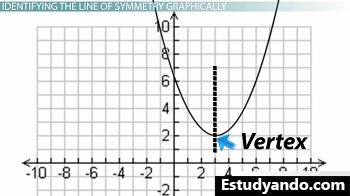
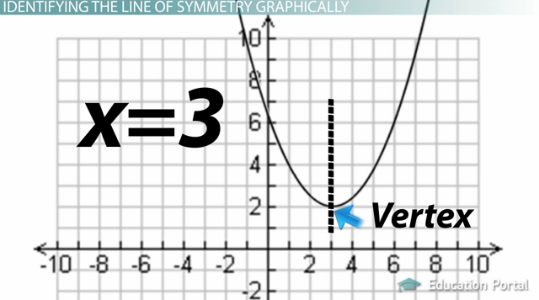
Kita dapat mengidentifikasi garis simetri secara grafis hanya dengan mencari titik terjauh pada kurva parabola. Ini disebut simpul , titik di mana dua garis terhubung. Jika parabola adalah sebuah bukit, titik tertinggi dari bukit itu akan mewakili puncak parabola, atau jika parabola adalah lembah, titik terendah lembah akan mewakili puncak parabola.
Lihatlah bagan ini. Apakah Anda melihat simpulnya? Itu ada di titik (2, 3).
|
|
xyxyx
|
|
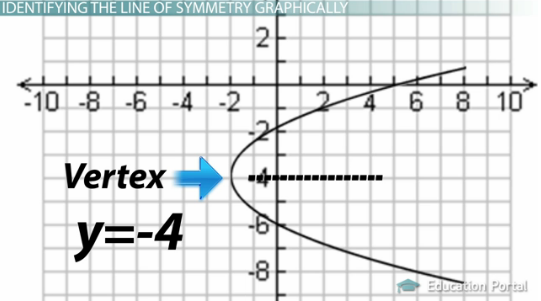
Oke, sekarang lihat grafik ini. Dapatkah Anda mengidentifikasi sumbu simetri? Titik puncaknya terletak di (-2, -4). Sekali lagi, dalam grafik ini, puncaknya adalah titik terendah parabola. Kita dapat menggambar garis imajiner melalui titik ini untuk menemukan garis simetri. Jadi kami akan menulis ini sebagai y = -4.
|
|
Identifikasi sumbu simetri secara aljabar
Anda akan paling sering melihat garis simetri dalam fungsi kuadrat. Fungsi kuadrat sering ditulis dalam bentuk standar y = ax ^ 2 + bx + c , dengan a , b , dan c sama dengan semua bilangan real. Semua fungsi kuadrat membuat parabola yang terbuka ke atas atau ke bawah.
Anda dapat mengidentifikasi sumbu simetri fungsi kuadrat dalam bentuk standar menggunakan rumus x = – b / 2 a . Mari kita lihat sebuah contoh.
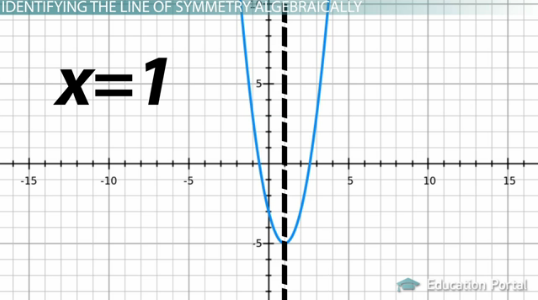
Untuk menemukan sumbu simetri persamaan ini, Anda harus memasukkan angka yang benar ke dalam rumus. Jadi persamaan kita adalah y = 2 x ^ 2 – 4 x – 3, dan bentuk standarnya adalah y = ax ^ 2 + bx + c . Jadi itu berarti a = 2 dan b = -4. Mari kita masukkan ke dalam rumus kita x = – b / 2 a , yang menghasilkan x = – (- 4/2 (2)). Sekarang evaluasi persamaannya. 2 x 2 = 4 dan – (- 4) / 4 = 4/4 = 1. Jadi sekarang kita memiliki 1, yang menghasilkan x = 1. Jika kita menggambar grafik persamaan ini, akan terlihat seperti ini.
|
|
Anda dapat melihat bahwa sumbu simetri melewati titik (1, -5).
Fungsi kuadrat juga dapat ditulis dalam bentuk simpul: y = ( x – h ) ^ 2 + k , dengan h = x dan k = y . Artinya h sama dengan koordinat x dan k sama dengan koordinat y dari titik tersebut. Lihatlah contoh ini.
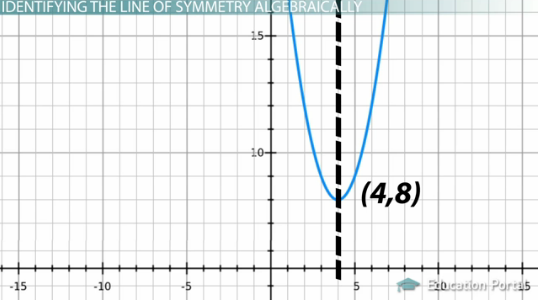
y = ( x – 4) ^ 2 + 8
Mereka cukup sederhana. Kita tahu bahwa dalam rumus simpul x = h , dan dalam persamaan ini h = 4, maka simpul kita adalah x = 4. Mengapa jawabannya positif 4 dan bukan negatif 4? Ingatlah bahwa h memiliki tanda negatif di depannya dalam persamaan titik puncak. Untuk menghindari kesalahan tanda, ingat trik cepat ini: Bayangkan angka itu dan tanda apa pun di depannya sebagai –h . Anda dapat membuat grafik persamaan untuk melihat letak titik puncak di titik (4, 8).
|
|
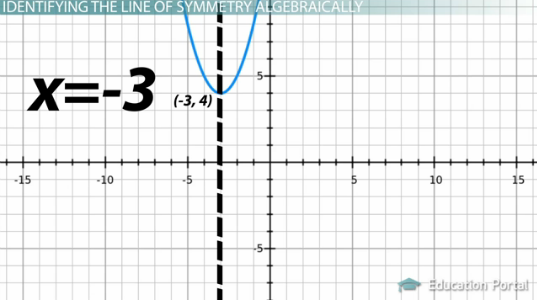
Coba persamaan ini. y = ( x + 3) ^ 2 + 4
Pertama, identifikasi –h . Kita dapat melihat dari persamaan ini bahwa -h = 3. Itu adalah 3 positif, jadi sekarang ambil kebalikan dari –h , yaitu -3, dan Anda memiliki sumbu simetri: x = -3.
|
|
Perhatikan grafik persamaan ini. Apakah Anda melihat sumbu simetri yang melewati titik (-3, 4)?
Ringkasan Pelajaran
Hari ini, Anda telah belajar tentang garis simetri, yaitu garis imajiner yang melewati pusat garis atau bentuk yang membentuk dua bagian yang sangat identik. Anda dapat menemukan sumbu simetri secara grafis atau aljabar. Untuk mencari garis simetri secara grafis, cari titik sudut, atau titik terjauh di mana dua garis terhubung, dan ketik x = atau y = lalu masukkan koordinat x atau y .
Untuk mencari garis simetri secara aljabar, Anda perlu mengidentifikasi apakah persamaan tersebut ditulis dalam bentuk standar atau dalam bentuk titik sudut. Bentuk standarnya adalah y = ax ^ 2 + bx + c , di mana a , b , dan c sama dengan semua bilangan real. Anda dapat menggunakan rumus x = – b / 2 a untuk mencari sumbu simetri. Bentuk puncaknya adalah y = ( x – h ) ^ 2 + k . di mana h = x dan k = y . Tentukan angka mana yang merupakan -h dalam persamaan, lalu tulis kebalikan dari -h untuk garis simetri Anda.
hasil pembelajaran
Pada akhir pelajaran ini, Anda harus dapat:
- Identifikasi garis simetri dalam contoh dunia nyata dan dalam grafik.
- Menghitung garis simetri dalam persamaan kuadrat